บ้าน บล็อก~~คู่มือรายละเอียดเกี่ยวกับ adder เต็มรูปแบบ~~

~~บน 10/05/2024~~ ~~628~~

คู่มือรายละเอียดเกี่ยวกับ adder เต็มรูปแบบ

ในขอบเขตของอุปกรณ์อิเล็กทรอนิกส์ดิจิตอลและวิศวกรรมคอมพิวเตอร์ Adders เป็นหนึ่งในหน่วยการสร้างที่สำคัญที่สุดคือสำคัญในการก่อสร้างและการทำงานของวงจรเลขคณิตที่ซับซ้อนยิ่งขึ้นในฐานะที่เป็นส่วนประกอบที่สำคัญของหน่วยเลขคณิต (ALU) เพิ่มการดำเนินการคอมพิวเตอร์จำนวนมากตั้งแต่เลขคณิตพื้นฐานไปจนถึงงานเชิงตรรกะที่ซับซ้อนที่จำเป็นสำหรับการดำเนินงานของระบบการออกแบบของพวกเขาซึ่งอาจแตกต่างกันไปจากผู้เพิ่มครึ่งหนึ่งไปจนถึงเพิ่มที่ซับซ้อนมากขึ้นมีบทบาทสำคัญในการเพิ่มประสิทธิภาพและความเร็วของการประมวลผลภายในระบบดิจิตอลบทความนี้นำเสนอสถาปัตยกรรมโดยละเอียดและความแตกต่างของฟังก์ชั่นของ Adders ประเภทต่าง ๆ แสดงให้เห็นถึงบทบาทที่สำคัญของพวกเขาในเทคโนโลยีการคำนวณที่ทันสมัยและสำรวจตรรกะการดำเนินงานวงจรและแอปพลิเคชันภายในบริบทที่กว้างขึ้นของการออกแบบตรรกะดิจิทัล

แคตตาล็อก

1. adder คืออะไร?

2. ครึ่งแอดเดอร์

3. Adder เต็มรูปแบบ

4. ตารางความจริง Adder เต็มรูปแบบ

5. สมการลักษณะของ adder เต็มรูปแบบ

6. การใช้วงจร adder เต็มรูปแบบ

7. ข้อดีและข้อเสียของสารเติมเต็มเต็มรูปแบบ

8. แอปพลิเคชันของ Adders เต็มรูปแบบในตรรกะดิจิตอล

9. ตัวอย่างของการใช้งาน adder เต็มรูปแบบ

10. บทสรุป

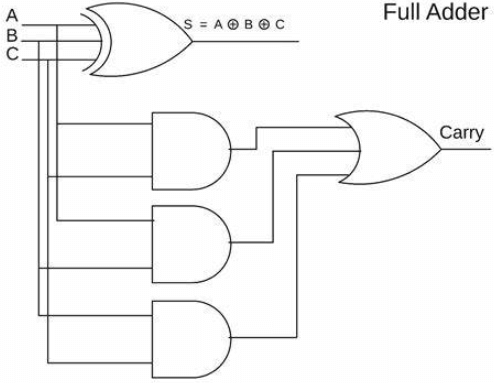
รูปที่ 1: Adder เต็มรูปแบบ

adder คืออะไร?

Adder เป็นองค์ประกอบพื้นฐานในด้านวิศวกรรมอิเล็กทรอนิกส์และการออกแบบตรรกะดิจิตอลและมีบทบาทสำคัญในระบบคอมพิวเตอร์ที่ซับซ้อนมากขึ้นในฐานะที่เป็นส่วนหนึ่งของหน่วยตรรกะเลขคณิต (ALU) Adder จัดการงานคอมพิวเตอร์ที่จำเป็นที่หลากหลายประสิทธิภาพและประสิทธิภาพของโปรเซสเซอร์ทั้งหมดได้รับผลกระทบโดยตรงจากการออกแบบและการทำงานของ Adder

ในโปรเซสเซอร์ Adder ไม่เพียง แต่ใช้สำหรับการดำเนินการทางคณิตศาสตร์ขั้นพื้นฐานเช่นการเพิ่มและการลบ แต่ยังมีส่วนร่วมในการดำเนินงานเชิงตรรกะที่กว้างขึ้นตัวอย่างเช่นเมื่อเรียกใช้โปรแกรมโปรเซสเซอร์มักจะต้องคำนวณที่อยู่หน่วยความจำใหม่โดยทั่วไปจะทำโดยการเพิ่มหรือลบออกจากที่อยู่ปัจจุบัน - งานที่ดำเนินการโดย Adderพวกเขาควบคุมจำนวนการวนซ้ำลูปและการไหลโดยรวมโดยการเพิ่มและลดลงของตัวนับในแอปพลิเคชันที่ซับซ้อนมากขึ้นเช่นการจัดทำดัชนีตารางเพิ่มการค้นหาข้อมูลอย่างรวดเร็วโดยการคำนวณออฟเซ็ตนี่เป็นสิ่งสำคัญสำหรับระบบการจัดการฐานข้อมูลการสร้างคอมไพเลอร์และการประมวลผลข้อมูลขนาดใหญ่นอกจากนี้ยังมีกุญแจสำคัญในการใช้เทคนิคการแมปบางอย่างในระบบแคชหลายระดับโดยใช้การดำเนินการทางคณิตศาสตร์เพื่อกำหนดตำแหน่งของข้อมูลในแคชซึ่งเป็นการเพิ่มประสิทธิภาพการเข้าถึง

เทคโนโลยีการเพิ่มจะถูกนำไปใช้ผ่านการออกแบบวงจรต่าง ๆ รวมถึง Adders คู่ขนานอนุกรมและท่อAdders แบบขนานได้รับการสนับสนุนสำหรับความสามารถในการจัดการตัวเลขหลายหลักพร้อมกันทำให้เหมาะสำหรับสถานการณ์ที่ต้องใช้การคำนวณอย่างรวดเร็วในทางกลับกัน Adders แบบอนุกรมประมวลผลหนึ่งบิตต่อรอบนาฬิกาและเหมาะสำหรับสภาพแวดล้อมที่ จำกัด ทรัพยากรหรือพลังงานต่ำAdders Pipeline แบ่งกระบวนการเพิ่มออกเป็นหลายขั้นตอนแต่ละการจัดการส่วนหนึ่งของการดำเนินการเพิ่มเติมการออกแบบนี้ช่วยเพิ่มความเร็วในการคำนวณโดยเฉพาะอย่างยิ่งในสภาพแวดล้อมการคำนวณประสิทธิภาพสูง

ครึ่งแอดเดอร์

วงจรครึ่งตัวปรับเป็นหน่วยการสร้างพื้นฐานในอุปกรณ์อิเล็กทรอนิกส์ดิจิตอลที่ออกแบบมาโดยเฉพาะเพื่อเพิ่มตัวเลขไบนารีสองตัวเดียววงจรนี้เป็นรากฐานของ adder เต็มรูปแบบและเป็นกุญแจสำคัญในการทำความเข้าใจการออกแบบวงจรตรรกะที่ซับซ้อนมากขึ้นใน Adder ครึ่งหนึ่งมีอินพุตหลักสองตัวที่มีป้ายกำกับ A และ B ซึ่งเป็นตัวแทนของ Augend และ Addend ตามลำดับการตั้งค่านี้ช่วยให้สามารถคำนวณผลรวมและดำเนินการส่งออกโดยไม่จำเป็นต้องมีอินพุตพกพาจากการคำนวณก่อนหน้านี้

แกนกลางของตัวปรับครึ่งประกอบด้วยประตูตรรกะสองประตู: ประตู XOR และประตูและประตูประตู XOR รับผิดชอบในการสร้างผลรวมเอาต์พุตมันทำงานภายใต้กฎง่าย ๆ ที่จะส่งออก 1 ถ้าเพียงหนึ่งในอินพุตของมันคือ 1;มิฉะนั้นจะส่งออก 0 และเกตในทางกลับกันจัดการเอาต์พุตเอาต์พุตมันผลิต 1 เฉพาะเมื่อทั้งสองอินพุตเป็น 1 ซึ่งสอดคล้องกับข้อกำหนดพื้นฐานของการเพิ่มไบนารี

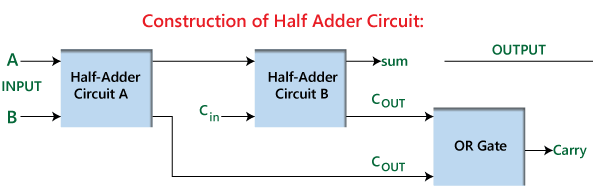
รูปที่ 2: การก่อสร้าง Adder ครึ่งหนึ่ง

การออกแบบที่มีประสิทธิภาพและตรงไปตรงมานี้ช่วยให้ Adder ครึ่งหนึ่งไม่เพียง แต่จะทำการเพิ่มไบนารีขั้นพื้นฐานอย่างอิสระ แต่ยังทำหน้าที่เป็นหน่วยการสร้างสำหรับการสร้าง adder เต็มAdder เต็มรูปแบบถูกสร้างขึ้นโดยการรวม Adders ครึ่งครึ่งเข้ากับประตูเพิ่มเติมหรือประตูในการตั้งค่านี้ Adder ครึ่งแรกจะใช้งานเพิ่มเติมเริ่มต้นสร้างผลรวมเบื้องต้นและการพกพาAdder ครึ่งหลังจากนั้นจะประมวลผลการพกพาจากครั้งแรกพร้อมกับอินพุตพกพาเพิ่มเติมในที่สุดหรือเกตจะรวมเอาท์พุททั้งสองเพื่อผลิตเอาต์พุตการพกพาสุดท้ายการจัดเรียงนี้ช่วยเพิ่มฟังก์ชั่นของ Adder ทำให้สามารถจัดการงานเพิ่มเติมได้หลายบิตที่ซับซ้อนมากขึ้นแสดงแอปพลิเคชันที่แพร่หลายและความสำคัญของการเพิ่มครึ่งหนึ่งในการออกแบบวงจรดิจิตอล

เต็ม adder

Adder เต็มรูปแบบเป็นส่วนประกอบขั้นสูงในการออกแบบตรรกะดิจิตอลพร้อมที่จะจัดการกับการเพิ่มอินพุตไบนารีบิตเดี่ยวสามอินพุตโดยทั่วไปที่ระบุว่าเป็น A, B และพกพา (CIN)การออกแบบนี้ช่วยให้ adder เต็มรูปแบบสามารถประมวลผลการเพิ่มไบนารีที่ซับซ้อนได้อย่างมีประสิทธิภาพโดยการรวมการพกพาจากการคำนวณลำดับล่างก่อนหน้านี้เข้ากับการดำเนินการเดียว

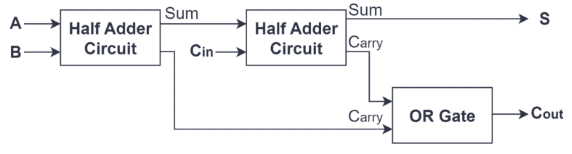
รูปที่ 3: วงจร adder เต็มรูปแบบ

ในทางปฏิบัติแล้ว Adder เต็มรูปแบบสามารถส่งผลรวมสองหลักซึ่งหมายความว่าเอาต์พุตของมันสามารถอยู่ในช่วงตั้งแต่ 0 ถึง 3 และยังสามารถสร้างพกพาออก (cout)สิ่งนี้เกิดขึ้นเพราะเมื่อบิตอินพุตทั้งหมดถูกตั้งค่าเป็น 1 (a = 1, b = 1, cin = 1) เอาต์พุตผลรวมจะเป็น 1 (แสดงไบนารี 01) และมีการสร้าง 1 ออกมาแสดงว่าต้องมีการพกพาเพิ่มเติมไปยังบิตที่สูงขึ้นถัดไป

โดยทั่วไปแล้ว adder เต็มรูปแบบประกอบด้วยสองส่วนเสริมครึ่งหนึ่งและหนึ่งหรือประตูAdder ครึ่งแรกใช้อินพุต A และ B สร้างผลรวมเริ่มต้นและสัญญาณพกพาผลรวมเริ่มต้นนี้จะถูกป้อนพร้อมกับพกพา (CIN) ลงในครึ่งหลังบทบาทของ Adder ในช่วงครึ่งหลังคือการเพิ่มผลรวมนี้จากครึ่งแรกของ Adder ไปยัง CIN สร้างผลรวมอีกครั้งและเอาต์พุตพกพาใหม่ในขณะเดียวกันการส่งออกจากครึ่งแรกของ adder และเอาต์พุตการพกพาจากครึ่งหลัง adder จะถูกรวมเข้าด้วยกันผ่านหรือประตูซึ่งจะปิดท้ายในการพกพาสุดท้าย (cout) ของ adder เต็มการออกแบบโครงสร้างนี้ช่วยให้มั่นใจได้ว่า Adder เต็มรูปแบบจัดการการแพร่กระจายของผู้ให้บริการอย่างมีประสิทธิภาพนอกจากนี้ทำให้มันเหมาะสำหรับการดำเนินการเพิ่มเติมไบนารีแบบหลายบิตดังนั้นการออกแบบ Adder เต็มไม่เพียง แต่เร่งการประมวลผลข้อมูลและเพิ่มประสิทธิภาพ แต่ยังทำให้ความซับซ้อนของการใช้งานฮาร์ดแวร์ง่ายขึ้นผ่านการรวมกันของประตูตรรกะที่ตรงไปตรงมาทำให้เป็นส่วนประกอบที่ขาดไม่ได้).

พารามิเตอร์	ครึ่งแอดเดอร์	เต็ม adder
คำอธิบาย	Half Adder เป็นตรรกะแบบผสมผสาน วงจรที่เพิ่มตัวเลข 1 บิตสองตัวHalf-adder สร้างผลรวมของทั้งสอง อินพุต	Adder เต็มรูปแบบเป็นตรรกะแบบผสมผสาน วงจรที่ดำเนินการเพิ่มเติมเกี่ยวกับตัวเลขไบนารีแบบหนึ่งบิตสามตัว Adder เต็มรูปแบบสร้างผลรวมของอินพุตทั้งสามและค่าพกพา
พกพาก่อนหน้า	ไม่ได้ใช้พกพาก่อนหน้า	ใช้พกพาก่อนหน้านี้
อินพุต	ในครึ่ง adder มีสองบิตอินพุต (a, b)	ใน adder เต็มมีบิตอินพุตสามบิต (A, B, C_ใน-
เอาต์พุต	เอาต์พุตที่สร้างขึ้นเป็นสองบิตซม และดำเนินการจากอินพุตของ 2 บิต	เอาต์พุตที่สร้างขึ้นเป็นสองบิตซม และดำเนินการจากอินพุต 3 บิต
ใช้เป็น	ไม่สามารถใช้วงจรครึ่งตัวต่อไปได้ เช่นเดียวกับวงจรเต็มรูปแบบ	สามารถใช้วงจร adder เต็มรูปแบบได้ ของวงจร adder ครึ่ง
คุณสมบัติ	มันง่ายและง่ายต่อการใช้งาน	การออกแบบ adder เต็มไม่ได้เป็น เรียบง่ายเหมือน Adder ครึ่ง
นิพจน์เชิงตรรกะ	นิพจน์ตรรกะสำหรับ Adder ครึ่งคือ: s = a⊕b;c = a*b	นิพจน์เชิงตรรกะสำหรับ adder เต็มคือ: s = a⊕b⊕cin;ค_ออก= (ab)+(c_ใน(a⊕b))
ประตูตรรกะ	ประกอบด้วยหนึ่งประตูเก่าหรือหนึ่งและหนึ่งและ ประตู.	ประกอบด้วยสองอดีตหรือสองและประตู และหนึ่งประตู
แอปพลิเคชัน	มันถูกใช้ในเครื่องคิดเลขคอมพิวเตอร์ อุปกรณ์วัดดิจิตอล ฯลฯ	มันถูกใช้ในการเพิ่มเติมหลายบิต โปรเซสเซอร์ดิจิทัล ฯลฯ
ชื่อสำรองของ	ไม่มีชื่ออื่นสำหรับครึ่ง adder.	Adder เต็มรูปแบบเป็นที่รู้จักกันในชื่อ Ripple-carry adder.

แผนภูมิ 1: ความแตกต่างระหว่าง Adder Half Adder และ Full Adder

ตารางความจริง Adder เต็มรูปแบบ

ตารางความจริงของ Adder เต็มรูปแบบเป็นกุญแจสำคัญในการทำความเข้าใจตรรกะการดำเนินงานโดยมีรายละเอียดความสัมพันธ์ที่แม่นยำระหว่างการรวมอินพุตไบนารีและเอาต์พุตที่สอดคล้องกันตารางนี้แสดงให้เห็นถึงสถานการณ์การป้อนข้อมูลที่เป็นไปได้ทั้งหมดและผลลัพธ์ของพวกเขาทำให้เป็นเครื่องมือสำคัญในการออกแบบและการตรวจสอบวงจรลอจิกดิจิตอลAdder เต็มรูปแบบจะประมวลผลอินพุตสามอินพุต: A, B และพกพา (CIN) ซึ่งแต่ละรายการอาจเป็น 0 หรือ 1 ซึ่งส่งผลให้เกิดการผสมผสานที่เป็นไปได้แปดประการของอินพุต

สำหรับชุดค่าผสมเหล่านี้แต่ละรายการเอาต์พุตจาก Adder เต็มรูปแบบรวมถึงผลรวม (ผลรวม) และการพกพา (cout)ผลรวมคือการเพิ่ม Modulo-2 (การดำเนินการ XOR) ของอินพุตทั้งสาม-A, B และ CINการดำเนินการเกิดขึ้นเมื่ออย่างน้อยสองบิตอินพุตคือ 1 สิ่งนี้สะท้อนให้เห็นถึงความสามารถของ Adder เต็มรูปแบบในการจัดการการพกพาในการดำเนินการต่อเนื่องเพื่อให้มั่นใจได้ถึงความแม่นยำในการคำนวณบิตที่สูงขึ้น

ในการแสดงให้พิจารณาสถานการณ์อินพุตที่อินพุตทั้งหมดเป็น 0 (a = 0, b = 0, c-in = 0)ผลรวมเอาท์พุทจะเป็น 0 และการพกพาจะเป็น 0 แสดงว่าไม่มีผลรวมหรือการจัดการเพิ่มเติมเพิ่มเติมหากมีเพียงหนึ่งบิตอินพุตคือ 1 เช่น A = 1, B = 0, C-in = 0 ผลรวมเอาต์พุตจะเป็น 1 โดยไม่มีการพกพาแสดงว่าไม่จำเป็นต้องถ่ายโอนการพกพาไปยังบิตที่สูงขึ้นเมื่อบิตอินพุตสองบิตคือ 1 เช่น A = 1, B = 1, C-in = 0 ผลรวมเอาต์พุตคือ 0 (ตั้งแต่ 1+1 เท่ากับ 2 ในไบนารีและโมดูโล 2 ส่งผลใน 0) แต่พกพา-ออกคือ 1 ซึ่งบ่งบอกถึงการพกพาที่จะต้องส่งผ่านไปยังบิตที่สูงขึ้นถัดไปสถานการณ์ที่ซับซ้อนที่สุดเกิดขึ้นเมื่อบิตอินพุตทั้งสามบิตคือ 1 (a = 1, b = 1, c-in = 1);ผลรวมเอาท์พุทคือ 1 และมีการพกพา 1 ครั้งโดยบอกว่าอาจจำเป็นต้องมีการจัดการพกพาที่บิตที่สูงขึ้น

อัน	ข	ค_ใน	S	ค_ออก
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

แผนภูมิที่ 2: ตารางความจริง Adder เต็มรูปแบบ

สมการลักษณะของ adder เต็มรูปแบบ

การทำความเข้าใจกับ adder เต็มรูปแบบเกี่ยวข้องกับการผ่าฟังก์ชันการทำงานโดยใช้ตารางความจริงที่การรวมกันของค่าอินพุตที่แตกต่างกัน a, b และ c-in นำไปสู่ผลรวมเอาต์พุตและ coutในการเข้าใจการดำเนินการเราทำให้สมการตรรกะง่ายขึ้นทีละขั้นตอน

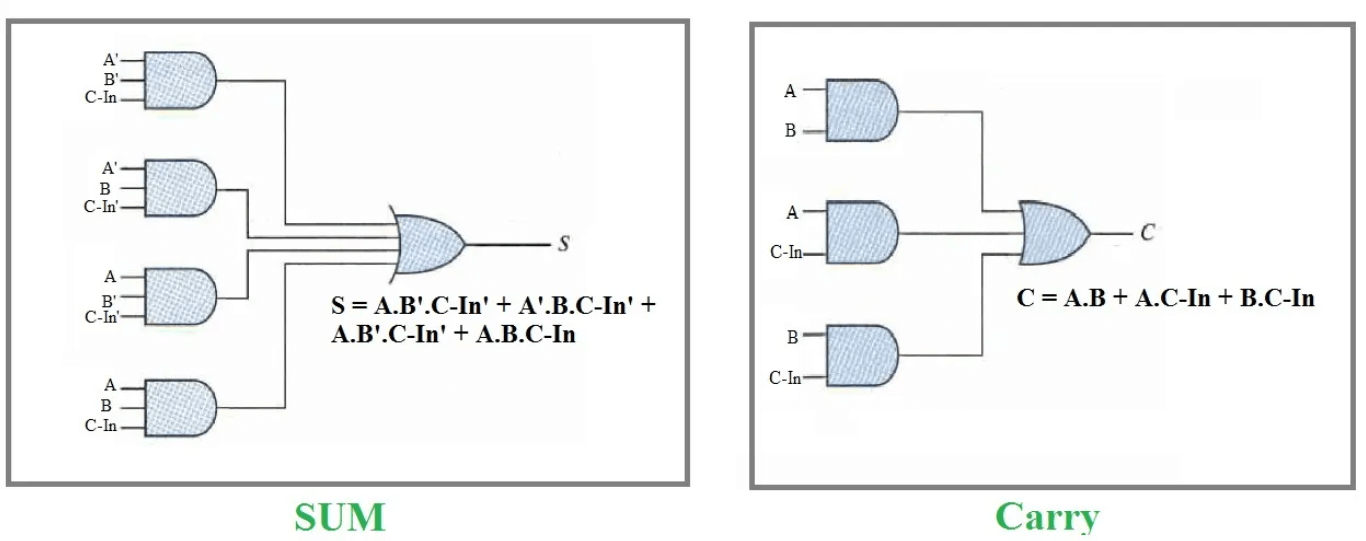
นิพจน์ตรรกะสำหรับผลรวม

สมการเริ่มต้นด้วยกรณีที่แตกต่างกันซึ่งผลรวมเท่ากับ 1:

• A 'B' CIN + A 'B CIN' + A B 'CIN' + AB CIN

สมการนี้สามารถย่อได้โดยการจัดกลุ่มเงื่อนไขที่มีและไม่มี CIN:

• cin (a 'b' + ab) + cin '(a' b + a b ')

การทำให้เข้าใจง่ายนี้นำไปสู่รูปแบบที่ง่ายต่อการใช้งาน:

• CIN XOR (A XOR B)

การเป็นตัวแทนนี้แสดงให้เห็นว่าเอาต์พุตผลรวมนั้นเป็นการดำเนินการ XOR ในหมู่ A, B และ CIN โดยจับพฤติกรรมหลักของการเพิ่มไบนารีซึ่งการสลับผลรวมตามจำนวนคี่

ตรรกะสำหรับ Cout

เริ่มต้นด้วยเงื่อนไขที่สร้างการพกพา:

• A 'B CIN + A B' CIN + AB C-IN ' + AB CIN

การทำให้สมการง่ายขึ้นเราระบุคำศัพท์ที่มักเกี่ยวข้องกับการสร้างพกพา:

• AB + B CIN + A CIN

กำลังมองหาวิธีอื่นในการใช้ cout สมการสามารถจัดระเบียบใหม่:

• ab + a cin + b c-in (a + a ')

สิ่งนี้จะขยายและรวมตัวกันใหม่เพื่อจับภาพสถานการณ์ทั้งหมดที่อย่างน้อยสองอินพุตคือ 1:

• ab cin + ab + a c-in + a 'b cin

• ab (1 + cin) + a c-in + a 'b cin

• ab + a c-in (b + b ') + a' b cin

• ab + a b 'cin + a' b cin

• AB + CIN (A 'B + A B')

แบบฟอร์มกะทัดรัดสุดท้ายสำหรับ Cout:

• AB + CIN (A XOR B)

สมการพกพารุ่นนี้แสดงให้เห็นว่าการผลิต cout นั้นเกิดขึ้นได้อย่างไรเมื่อทั้ง A และ B เป็น 1 หรือเมื่อหนึ่งใน A หรือ B คือ 1 พร้อมกับพกพาดังนั้นจึงห่อหุ้มตรรกะที่จำเป็นในการจัดการการแพร่กระจายการเพิ่มไบนารีบิตตรรกะที่มีความคล่องตัวนี้มีประโยชน์อย่างยิ่งสำหรับการใช้วงจรดิจิตอลที่มีประสิทธิภาพ

รูปที่ 4: สมการของ adder เต็มรูปแบบ

การใช้วงจร adder เต็มรูปแบบ

การใช้วงจร adder เต็มรูปแบบนั้นเกี่ยวข้องกับการประกอบแอดเดอร์ครึ่งครึ่งอย่างระมัดระวังและเกตหรือเกตเพื่อสร้างอุปกรณ์ที่สามารถจัดการกับการเพิ่มอินพุตไบนารีแบบบิตเดี่ยวได้อย่างมีประสิทธิภาพการจัดเรียงนี้ช่วยเพิ่มประสิทธิภาพความซับซ้อนของวงจรและทำให้มั่นใจได้ว่าการคำนวณทั้งที่มีประสิทธิภาพและแม่นยำ

ในการเริ่มต้น Adder ครึ่งแรกใช้อินพุตไบนารีหลักสองตัวคือ A และ B ซึ่งเป็นตัวเลขหลักที่จะเพิ่มงานสำคัญคือการคำนวณผลรวมและการพกพาเริ่มต้นของตัวเลขสองตัวนี้ที่นี่ Adder ครึ่งแรกให้ผลลัพธ์สองรายการ: ผลรวมเริ่มต้น (SUM1) และพกพาเริ่มต้น (Carry1)SUM1 มาจากการทำงานของ XOR ของ A และ B ซึ่งระบุว่ายอดรวมมีจำนวนคี่ 1 หรือไม่Carry1 ผลลัพธ์ของการดำเนินการและการดำเนินการระหว่าง A และ B ระบุว่าตัวเลขทั้งสองเป็น 1 หรือไม่ซึ่งจำเป็นต้องมีการพกพาไปยังบิตที่สูงขึ้นถัดไป

ถัดไป Adder ครึ่งหลังเข้าร่วมกระบวนการมันใช้ผลรวมเอาต์พุต SUM1 และอินพุตที่สาม CIN (พกพาจากการคำนวณก่อนหน้า) เป็นอินพุตAdder ครึ่งหลังผลิตผลลัพธ์สองรายการ: ผลรวมสุดท้าย (SUM2) และพกพารอง (Carry2)SUM2 ซึ่งเป็นผลลัพธ์ XOR ของ SUM1 และ CIN แสดงถึงผลรวมสุดท้ายของอินพุตทั้งสามซึ่งแสดงการเพิ่มไบนารีโดยรวมCarry2 ที่เกิดขึ้นจากการดำเนินการระหว่าง SUM1 และ CIN หมายถึงการพกพาที่สร้างขึ้นโดยส่วนประกอบเหล่านี้

Full Adder Circuit with Using Two Half Adder

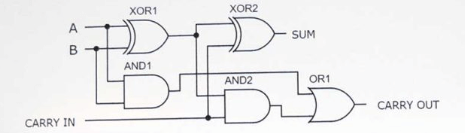
รูปที่ 5: วงจร adder เต็มรูปแบบโดยใช้ Adder สองครึ่ง

ในที่สุดเพื่อให้การออกแบบของ Adder เต็มรูปแบบหรือประตูจะต้องจัดการเอาท์พุทพกพาพกพา 1 และพกพา 2 จากทั้งสองส่วนเสริมประตูนี้หรือประตูนี้ช่วยให้มั่นใจได้ว่ามีการพกพาใด ๆ ที่สร้างขึ้นระหว่างการคำนวณจะถูกส่งต่อไปยังผลลัพธ์สุดท้ายอย่างถูกต้องดังนั้นการพกพาครั้งสุดท้ายของ Adder (Cout) จึงเป็นผลหรือผลของ Carry1 และ Carry2การรวมของประตูนี้รับประกันได้ว่าการดำเนินการที่มีศักยภาพทั้งหมดจะถูกคำนวณอย่างแม่นยำและถ่ายทอดไปยังระดับต่อไปในการดำเนินการเพิ่มหลายบิตเพื่อให้มั่นใจถึงความสมบูรณ์ของการดำเนินการทางคณิตศาสตร์ในหลายบิต

ข้อดีและความท้าทายของ Adders เต็มรูปแบบในตรรกะดิจิตอล

Adders เต็มรูปแบบมีบทบาทที่ขาดไม่ได้ในการออกแบบตรรกะดิจิทัลนำเสนอประโยชน์มากมายที่ทำให้พวกเขาจำเป็นในการคำนวณและสถานการณ์การประมวลผลข้อมูลต่างๆข้อได้เปรียบหลักของพวกเขารวมถึงความยืดหยุ่นที่น่าทึ่งความเร็วในการประมวลผลอย่างรวดเร็วและการจัดการพกพาที่มีประสิทธิภาพลักษณะเหล่านี้ทำให้ส่วนเสริมเต็มรูปแบบเหมาะสำหรับการดำเนินการทางคณิตศาสตร์ที่ซับซ้อนและฟังก์ชั่นตรรกะโดยเฉพาะอย่างยิ่งในแอปพลิเคชันที่ต้องเพิ่มหลายบิตตามลำดับ

ข้อดี

ความยืดหยุ่น: Adders เต็มรูปแบบมีความสามารถในการประมวลผลอินพุตไบนารีหลายตัว (A, B และ CIN) พร้อมกันพวกเขายังสามารถขยายเป็นอาร์เรย์ adder ขนาดใหญ่เพื่อจัดการตัวเลขไบนารีที่ยาวขึ้นความสามารถในการปรับขนาดนี้มีความสำคัญสำหรับการสร้างหน่วยตรรกะเลขคณิตประสิทธิภาพสูง (ALUS) ซึ่งจะต้องดำเนินการเลขคณิตหลายบิตและตรรกะที่ซับซ้อน

ความเร็ว: ด้วยสถาปัตยกรรมการประมวลผลแบบขนานภายในของพวกเขาเพิ่มการเติมเต็มสามารถเติมอินพุตทั้งหมดในรอบนาฬิกาเดียวในขณะเดียวกันก็กำหนดว่าจะมีเอาต์พุตความสามารถนี้รองรับการเพิ่มการดำเนินการอย่างต่อเนื่องและเป็นสิ่งที่ขาดไม่ได้สำหรับการประมวลผลข้อมูลแบบเรียลไทม์ในไมโครโปรเซสเซอร์ที่ทันสมัยและอุปกรณ์คอมพิวเตอร์ความเร็วสูง

ข้อเสีย

อย่างไรก็ตามสารเติมเต็มเต็มยังนำเสนอข้อเสียที่น่าสังเกต:

ความซับซ้อนในการออกแบบและการใช้งาน: Adders เต็มรูปแบบเกี่ยวข้องกับประตูตรรกะหลายแห่งและการแพร่กระจายการพกพาหลายระดับทำให้การออกแบบที่ซับซ้อนความซับซ้อนนี้ไม่เพียง แต่เพิ่มต้นทุนการผลิต แต่ยังสามารถส่งผลกระทบต่อความน่าเชื่อถือของวงจร

ปัญหาการหน่วงเวลาการแพร่กระจาย: พกพาการแพร่กระจายอาจผ่านประตูตรรกะหลายแห่งแต่ละครั้งเพิ่มความล่าช้าสิ่งนี้สามารถ จำกัด ความเร็วในการคำนวณโดยรวมในระหว่างการดำเนินงานขนาดใหญ่โดยเฉพาะอย่างยิ่งในระบบคอมพิวเตอร์ที่กว้างขวางและในการออกแบบการรวมขนาดใหญ่มาก (VLSI) และโปรเซสเซอร์ความเร็วสูงความล่าช้าสามารถกลายเป็นคอขวดที่สำคัญในประสิทธิภาพ

เพื่อลดปัญหาเหล่านี้วิศวกรสำรวจการออกแบบวงจรที่มีประสิทธิภาพมากขึ้นอย่างต่อเนื่องกลยุทธ์รวมถึงการใช้เทคโนโลยีประตูตรรกะที่เร็วขึ้นการปรับเค้าโครงวงจรให้เหมาะสมเพื่อลดความยาวเส้นทางและการพัฒนาเทคโนโลยีขั้นสูงเช่นอุปกรณ์เสริมแบบพกพาเพื่อลดความล่าช้าในการขยายพันธุ์

แอปพลิเคชันของ Adders เต็มรูปแบบในตรรกะดิจิตอล

Adders เต็มรูปแบบจะถูกนำมาใช้อย่างกว้างขวางในตรรกะดิจิตอลที่มีค่าสำหรับความยืดหยุ่นและประสิทธิภาพทำให้พวกเขาเป็นศูนย์กลางของงานคอมพิวเตอร์และการประมวลผลข้อมูลมากมายแอปพลิเคชันของพวกเขาครอบคลุมตั้งแต่การดำเนินการทางคณิตศาสตร์พื้นฐานไปจนถึงการประมวลผลสัญญาณที่ซับซ้อนและการควบคุมระบบนี่คือภาพรายละเอียดบางส่วนที่สำคัญที่เสริมเต็มรูปแบบ

วงจรเลขคณิต

หนึ่งในการใช้งานที่ตรงไปตรงมาที่สุดของ Adder Full คือในวงจรเลขคณิตที่พวกเขาทำการเพิ่มไบนารีโดยเฉพาะอย่างยิ่งสิ่งสำคัญในการเพิ่มจำนวนหลายบิตตัวเพิ่มเต็มรูปแบบจัดการลำดับไบนารีที่ยาวขึ้นผ่านการเรียงซ้อนในการจัดเรียงนี้ Adder เต็มรูปแบบแต่ละตัวจัดการการเพิ่มตำแหน่งบิตและการพกพาจากบิตล่างจากนั้นผ่านการพกพาใหม่ไปยัง Adder เต็มของบิตที่สูงขึ้นถัดไปน้ำตกนี้ช่วยให้การเพิ่มหลายบิตที่ครอบคลุมทั่วทั้งตัวเลขทั้งหมด

การประมวลผลข้อมูล

Adders เต็มรูปแบบยังมีบทบาทสำคัญในงานการประมวลผลข้อมูลขั้นสูงเช่นการประมวลผลสัญญาณดิจิตอล (DSP) สำหรับการกรองและการแปลงฟูริเยร์ซึ่งจำเป็นต้องมีการดำเนินการทางคณิตศาสตร์ที่แม่นยำและรวดเร็วนอกจากนี้ในขอบเขตของความปลอดภัยของข้อมูลรวมถึงการเข้ารหัสข้อมูลและการตรวจจับข้อผิดพลาดและอัลกอริธึมการแก้ไขเช่นการตรวจสอบความเท่าเทียมและการสร้างรหัสการตรวจสอบความซ้ำซ้อน (CRC) แบบเต็มรูปแบบ

เคาน์เตอร์

ในเคาน์เตอร์ดิจิตอลสารเติมเต็มเต็มนั้นขาดไม่ได้สำหรับการใช้งานฟังก์ชั่นการเพิ่มขึ้นและการลดลงโดยเฉพาะอย่างยิ่งในเคาน์เตอร์แบบแยกส่วนและแบบซิงโครนัสพวกเขาจัดการอย่างถูกต้องถือและยืมเพื่อให้แน่ใจว่ามีการนับอย่างแม่นยำ

มัลติเพล็กเซอร์ (mux) และ demultiplexers (demux)

ในมัลติเพล็กเซอร์และ demultiplexers ส่วนเสริมเต็มมีบทบาทสำคัญในการเลือกช่องและการกระจายข้อมูลพวกเขามีส่วนร่วมในตรรกะที่กำหนดว่าช่องใดที่ใช้สำหรับการป้อนข้อมูลและเอาต์พุตการตัดสินใจตามสัญญาณควบคุมตรรกะ

เทคโนโลยีหน่วยความจำ

ในการกำหนดที่อยู่หน่วยความจำ Adders แบบเต็มช่วยสร้างสัญญาณที่อยู่สำหรับการเข้าถึงตำแหน่งหน่วยความจำแบบไดนามิกสิ่งนี้มีความสำคัญอย่างยิ่งในหน่วยความจำแบบสุ่มแบบไดนามิก (DRAM) และระบบจัดเก็บข้อมูลอื่น ๆ ซึ่งส่วนเสริมเต็มรูปแบบรองรับการคำนวณที่อยู่ที่ซับซ้อนเพื่อเพิ่มประสิทธิภาพของการเข้าถึงหน่วยความจำ

หน่วยตรรกะเลขคณิต (ALU)

ในที่สุดเป็นองค์ประกอบพื้นฐานของหน่วยตรรกะเลขคณิตในไมโครโปรเซสเซอร์และโปรเซสเซอร์สัญญาณดิจิตอลสารเติมเต็มเต็มมีความสำคัญALU จัดการการดำเนินการทางคณิตศาสตร์และตรรกะทั้งหมดด้วยการเสริมเต็มรูปแบบเพื่อให้มั่นใจว่าข้อมูลจะถูกประมวลผลทั้งอย่างรวดเร็วและแม่นยำ

ตัวอย่างของการใช้งาน adder เต็มรูปแบบ

Adders แบบเต็มสามารถสร้างได้โดยใช้ประตูลอจิกและการกำหนดค่าต่างๆที่นี่เราสำรวจการใช้งานที่แตกต่างกันสี่แบบเน้นการตั้งค่าและความแตกต่างในการปฏิบัติงาน

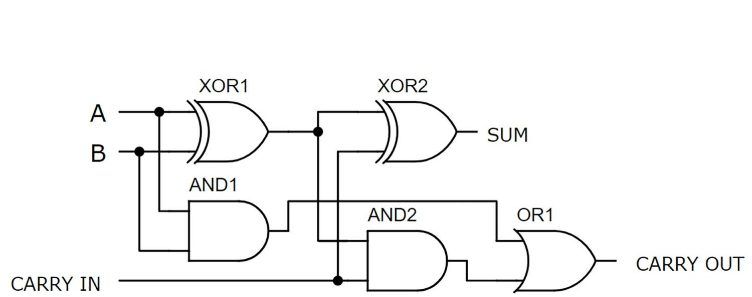
Adder เต็มรูปแบบสร้างด้วย XOR และและหรือประตู

Full Adder Built with XOR, AND, and OR Logic Gates

รูปที่ 6: Adder เต็มรูปแบบที่สร้างด้วย XOR และและหรือประตูตรรกะ

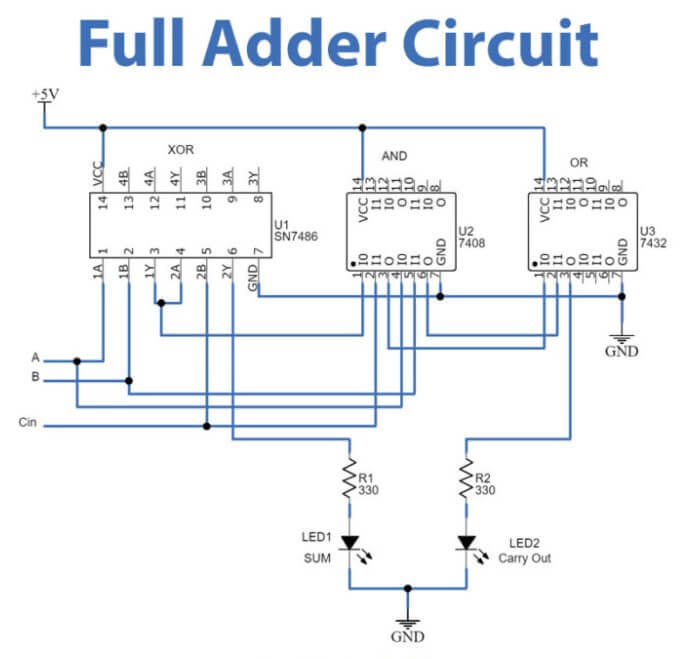
ตัวอย่างนี้นำเสนอ adder เต็มรูปแบบที่สร้างขึ้นบนกระดานข่าวโดยใช้ทรานซิสเตอร์ที่ไม่ต่อเนื่องการกำหนดค่าประกอบด้วยห้าประตูลอจิก: ประตู XOR สองประตูสองประตูและประตูและประตูหนึ่งประตูต้องใช้ทรานซิสเตอร์ทั้งหมด 21 ตัวอินพุต A และ B เชื่อมต่อกับด้านซ้ายบนของ Breadboard ได้รับการจัดหา A +5Vอินพุตเหล่านี้ถูกควบคุมโดยใช้สวิตช์สลับสองตัวLED สองตัวที่ด้านบนซ้ายระบุสถานะของอินพุต A และ B ในขณะที่ LED สองตัวที่ด้านขวาแสดงเอาต์พุตตัวต้านทานที่ใช้ในวงจรทั้งหมด 2.2k โอห์มเมื่ออินพุต A และ B เปิดอยู่และการพกพาปิดเอาต์พุตแสดงค่าไบนารี 10 ซึ่งแสดงถึงผลรวม 2 (1 + 1 + 0 = 10)Xor Gates สร้างขึ้นด้วยทรานซิสเตอร์ 12 ตัวแรกจัดการการรวมหลักในขณะที่ครึ่งล่างของเขียงหั่นขนมประกอบด้วยและและหรือหรือประตูสำหรับการดำเนินการพกพาการเดินสายรหัสสีช่วยเพิ่มความชัดเจนและการแก้ไขปัญหา

เต็ม adder โดยใช้ Nand Gates

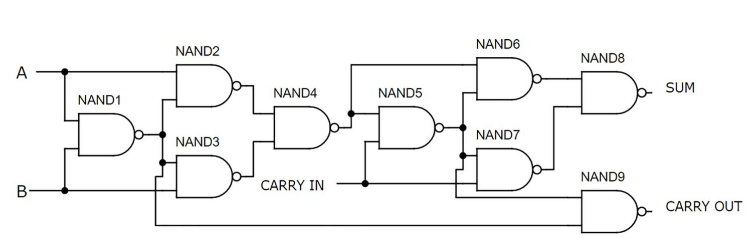
รูปที่ 7: Adder เต็มรูปแบบโดยใช้ Nand Gates

Adder เต็มรูปแบบนี้ใช้ประตู Nand เก้าประตูโดยแต่ละประตูทำจากสองทรานซิสเตอร์รวมเป็นจำนวน 18 ทรานซิสเตอร์วิธีนี้เป็นหนึ่งในวิธีที่ง่ายที่สุดและมีประสิทธิภาพมากที่สุดในการสร้าง adder เต็มรูปแบบโดยใช้ส่วนประกอบที่ไม่ต่อเนื่องประตูทั้งหมดจะประกอบอยู่ที่ครึ่งบนของเขียงหั่นขนมในขณะที่สวิตช์ครอบครองครึ่งล่างฟังก์ชั่นของวงจรแสดงให้เห็นด้วยอินพุต A และ B เปิดและการปิดการใช้งานส่งผลให้ค่าไบนารีเอาต์พุต 10 เทียบเท่ากับทศนิยม 2

เต็มไปด้วยประตูหรือประตู

รูปที่ 8: เต็มไปด้วยประตูหรือประตู

สร้างขึ้นด้วยเก้าหรือประตูแต่ละอันต้องการสองทรานซิสเตอร์การตั้งค่านี้ยังใช้ทรานซิสเตอร์ 18 ตัวทั้งหมดการสร้าง adder เต็มรูปแบบด้วย NOR Gates เป็นทางเลือกที่ดี แต่เกี่ยวข้องกับการเดินสายที่ซับซ้อนมากขึ้นเมื่อเทียบกับประตู NANDแต่ละทรานซิสเตอร์ใน NOR นั้นมีสายดินโดยมีนักสะสมที่เชื่อมต่อกันด้วยสายจัมเปอร์สีส้มเพื่อให้แน่ใจว่าการเดินสายที่เรียบร้อยและเป็นระเบียบการกำหนดค่านี้จะแสดงด้วยอินพุต A และ B เปิดใช้งานและการปิดการใช้งานพกพานำไปสู่เอาต์พุตที่การพกพาทำงานอยู่และผลรวมปิด

บทสรุป

ตลอดการสำรวจเทคโนโลยี Adder นี้ตั้งแต่ Adder ครึ่งพื้นฐานไปจนถึงการออกแบบ Adder เต็มรูปแบบที่ซับซ้อนจะเห็นได้ชัดว่าส่วนประกอบเหล่านี้เป็นพื้นฐานของความก้าวหน้าของอุปกรณ์อิเล็กทรอนิกส์ดิจิตอลลักษณะการปฏิบัติงานและตัวอย่างการดำเนินการให้การเน้นย้ำถึงความเก่งกาจและประสิทธิภาพของส่วนเสริมในการตั้งค่าการคำนวณที่หลากหลายโดยการตรวจสอบโครงสร้างและหน้าที่ของ Adders โดยเฉพาะอย่างยิ่งผ่านตารางความจริงและสมการลักษณะเฉพาะเราจะได้รับข้อมูลเชิงลึกที่มีค่าเกี่ยวกับความสามารถและข้อ จำกัด ของพวกเขาความรู้นี้มีประโยชน์ในการพัฒนาระบบคอมพิวเตอร์ที่มีประสิทธิภาพและเร็วขึ้นในที่สุดเพิ่มการคำนวณแบบไบนารีที่ซับซ้อนไม่เพียง แต่ช่วยให้การเพิ่มจำนวนของเทคโนโลยีในพื้นที่ที่มีความหลากหลายเช่นการประมวลผลข้อมูลการจัดสรรหน่วยความจำและการประมวลผลสัญญาณดิจิตอลในขณะที่เทคโนโลยีดิจิตอลวิวัฒนาการไปการปรับแต่งและนวัตกรรมอย่างต่อเนื่องในการออกแบบ Adder จะยังคงเป็นรากฐานที่สำคัญในการพัฒนาสถาปัตยกรรมการคำนวณขั้นสูงมากขึ้นเพื่อให้มั่นใจว่าส่วนประกอบพื้นฐานเหล่านี้ยังคงเป็นหัวใจสำคัญของการออกแบบระบบดิจิตอลและการใช้งาน

คำถามที่พบบ่อย [คำถามที่พบบ่อย]

1. วงจร adder เต็มคืออะไร?

Adder เต็มรูปแบบเป็นวงจรดิจิตอลที่เพิ่มบิตไบนารีสามบิตเพื่อสร้างผลรวมและเอาต์พุตพกพามันถูกออกแบบมาเพื่อจัดการการเพิ่มสามอินพุต: สองบิตที่สำคัญและหนึ่งบิตพกพาจากการเพิ่มก่อนหน้านี้สิ่งนี้จะช่วยให้สามารถใช้ในขั้นตอนต่อเนื่องเพื่อเพิ่มตัวเลขไบนารีหลายบิต

2. เท่าไหร่และหรือ xor ใน adder เต็ม?

adder เต็มทั่วไปประกอบด้วย:

ประตู XOR สองประตูสำหรับการสร้างผลรวม

สองและประตูที่จะมีส่วนร่วมในการคำนวณพกพา

หนึ่งหรือประตูเพื่อสรุปเอาต์พุตการดำเนินการ

3. อินพุตพกพาอะไรใน Adder เต็ม?

อินพุตพกพา (CIN) ใน Adder เต็มรูปแบบคือบิตพกพาจากการเพิ่มบิตที่สำคัญต่ำกว่าก่อนหน้านี้ในการเพิ่มไบนารีแบบหลายบิตช่วยให้ Adder เต็มรูปแบบพิจารณาการพกพาก่อนหน้านี้เมื่อคำนวณผลรวมปัจจุบันและการพกพาใหม่

4. ทำไมต้องใช้ adder เต็มแทน adder ครึ่ง?

adder เต็มรูปแบบถูกใช้แทน adder ครึ่งหนึ่งเพราะสามารถเพิ่มสามบิต (รวมถึงการพกพาจากการเพิ่มเติมก่อนหน้านี้) ทำให้เหมาะสำหรับการผูกมัดร่วมกันเพื่อเพิ่มจำนวนหลายบิตตัวปรับครึ่งสามารถเพิ่มสองบิตและไม่มีข้อกำหนดสำหรับการพกพาซึ่ง จำกัด การใช้งานในรูปแบบที่ง่ายที่สุดของการเติมไบนารีโดยไม่ต้องมีการแพร่กระจายแบบต่อเนื่อง

เกี่ยวกับเรา

ALLELCO LIMITED

Allelco เป็นจุดเริ่มต้นที่โด่งดังในระดับสากล ผู้จัดจำหน่ายบริการจัดหาของส่วนประกอบอิเล็กทรอนิกส์ไฮบริดมุ่งมั่นที่จะให้บริการการจัดหาและซัพพลายเชนส่วนประกอบที่ครอบคลุมสำหรับอุตสาหกรรมการผลิตและการจัดจำหน่ายอิเล็กทรอนิกส์ทั่วโลกรวมถึงโรงงาน OEM 500 อันดับสูงสุดทั่วโลกและโบรกเกอร์อิสระ
อ่านเพิ่มเติม